PICマイコンで電卓(設計・製作編2)
2016/09/28
前回の投稿から1月以上空いてしまい申し訳ありません。提出しないと人生が終わりかねない大切な論文の執筆で忙しかったものですから…
結局、まだ電卓のハードウェアの作成は終わっていませんので、今回は電卓のデータ構造ついて書いていこうと思います。
スポンサーリンク
実装する演算
前回(PICマイコンで電卓(設計・製作編1))、「29個のボタンを搭載」すると宣言しました。そこで、まずはこれらのボタンにどのような機能を割り当てるかを決定しましょう。
使用する16F84Aの性能を考慮しつつ比較的無理なく実装可能であろう、という機能を考えたところ次のようになりました。
- 数字キー(0~9)・・・10個
- メモリ機能(M+, M-, MR, MC, MS)・・・5個
- クリア機能(→, CE, AC)・・・3個
- 演算機能(+, -, ×, ÷, %, GT, x2, √, 税込, 税抜)・・・10個
- 演算実行・GT計算機能( = )・・・1個
(絶望的に価値がない電卓になっている気が…)
内部のデータ構造
使用するマイコンである16F84Aはとんでもなく低性能ですが、それでもコンピュータには違いありません。よって、人間にとって都合の良い「10進数」はマイコンではかなり扱いにくい形態になります。しかも、計算に用いることが出来る汎用レジスタ(8bit幅)は68個しかありません。したがって、効率よくPICマイコンで計算を行うためには、レジスタに直接2進数の形で値を格納して演算を行うのが好ましいと言えます。
しかしながら、PICマイコンの持ってるレジスタはすべて「8ビット幅」なので、(2の補数表現の場合)-128 ~ 127の値しか表すことが出来ません。4桁表示では-9999~9999の値を扱う必要がありますので、最低でも2つのレジスタを用いる必要があります。(2つのレジスタを用いれば-32768~32767の値を扱えますので、-9999~9999をカバーできます。 )
さらに今回の電卓には「掛け算」機能がありますが、16ビットの変数同士の掛け算を行った場合、計算結果は32ビットになりますので、すべての演算を32ビットで行うようにしておけば問題なさそうです。
以上をまとめると、
- 数字ボタンを入力されたら、その数字に該当する2進数を算出し、8ビットレジスタ2つ結合した16ビットレジスタに格納する。
- すべての演算は32ビット単位で行う。(ただし、基本的には下位16ビットのみを用い、掛け算などのときのみ32ビットすべてを使用する)
となります。
入力された10進数を2進数に変換する
電卓への入力は10進数表記の数字キーを用いて行われるわけですが、内部では2進数で演算を行うため、入力された数字を逐次2進数レジスタに放り込んでいかねばなりません。しかし先述の通り、16F84Aはお世辞にも高機能なマイコンとはいえないため、比較的軽い処理で入力された数字を2進数に直さねばなりません。そこで、まずは、入力された数字の特徴を抑えていきましょう。
例として、「5471」という4桁の数字を電卓に入力する場合を考えます。
(青字はユーザの入力、赤字は電卓の動作を表します。)
- ユーザは「5」のボタンを押します。
- 電卓のディスプレイの右端に「5」が表示されます。
- ユーザは続けて「4」のボタンを押します。
- 電卓のディスプレイに表示されていた「5」は1桁左にずれ、空いた右端の桁に「4」が表示され、全体の表示は「54」になります。
- ユーザは続けて「7」のボタンを押します。
- 電卓のディスプレイに表示されていた「54」は全体的に左に一桁ずれ、空いた右端の桁に「7」が表示され、全体の表示は「547」になります。
- ユーザは続けて「1」のボタンを押します。
- 電卓のディスプレイに表示されていた「547」は全体的に左に一桁ずれ、空いた右端の桁に「1」が表示され、全体の表示は「5471」になります。
1,2の「5」を入力された直後は、単純にレジスタに2進数で「5」を表す「0000 0000 0000 0101」を代入すればよいことになります。
次に「4」を入力されたときはどのようにすればよいでしょうか? それは、「4」が入力されたとき、表示されている「5」は一桁分左にずれます。10進数において、『一桁左にシフト』ということは、『値を10倍する』ことと等価なことを利用します。つまり、レジスタに保持されている「5」を10倍してやれば良いことになります。
さて、「10倍すればよい」と簡単に言いましたが、16F84Aには「掛け算機能」が備わっていません。よって、16F84Aに備わっている「シフト機能」と「加算機能」を用いて何とか「10倍」をでっち上げなければなりません。(当然ながら同じ数字を10回足す、とかいうおバカな方法は無しで・・・)
先ほど「10進数における左1桁シフトは10倍と等価」と申し上げました。同じ原理で、「2進数における左1桁シフトは2倍と等価」になります。したがって、我々が使える計算方法は「2倍」することと、「足し算」だけとなります。これらをうまく使って10倍する方法はあるのでしょうか?
結論から言うと、あります。 例えば、nという数字を10倍したいとき、 { (n×2×2)+n } ×2 をしてやれば10Aを得ることが出来ます。このことを利用すると、ある数字nを10倍するアルゴリズムは次のように表すことが出来ます。
- nを2ビット分左シフトし、シフト結果を適当なレジスタmに格納する。(右端の空いた桁には0を入れる。)
- mにシフト前のnを加算する。
- m自身を1ビット左シフトする。
この方法に従って、「5」を10倍すると次の図のようになります。
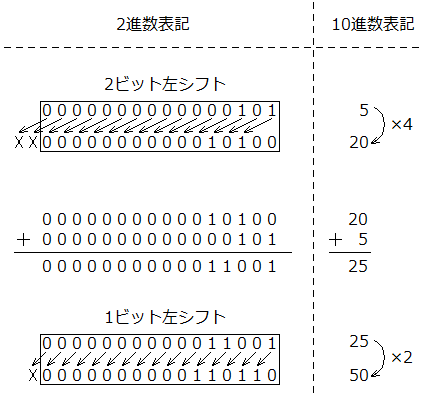
このように、シフト演算と加算のみを用いて3ステップで5*10=50が実行できています。
この「50」に入力された「4」を加算してやると、内部レジスタの値は「54」となります。以降の入力も同じように、「レジスタの値を10倍して入力値を加算」としてやれば、10進数で入力された値を逐次的に2進数に変換できます。
さて、今回は入力された値をどのようにして2進数に直すか確認しました。
次回は2進数に直された値を、どのように演算していくか見ていきましょう。