電子回路を扱うのに最低限必要な法則
電子工作を始めてみようと思う人にとって，本当に気になるのは「最小限どの程度の知識がいるの？」とか「中学物理程度でいいのか？」とかそういうことだと思います．というのは，いきなり人の作例を見ても，「なぜこの抵抗の値はこのように決めたのだろう」とか「このコンデンサは何のためにあるの？」という疑問が多く生まれ，いったいどんな知識を身に着けたらその謎が解けるのかすら不明な状態にあることが多いからです．
要するに「何が分かればわかるようになるのかわからない」状態ですね．
実際のところ，他の人が作った回路を全て理解するのは非常に難しく，分野によっては大学院で習うような内容を必要とすることもあります．しかし，何も私たちは「高校・大学・大学院で習うことを全て身に着けたい」訳ではなく，「あくまで電子回路を扱う上で必要な知識を身に着けたい」だけです．
そこで，小学校ないし中学校で習う「オームの法則」レベルの話しから実際に回路を組むのに必要な知識までを今後じわじわと紹介していけたらな，と思っています．
今回はその第一回，「最低限必要な法則である二つの数式」をご紹介したいと思います．
Contents
キルヒホッフの電流則
「キルヒホッフの電流則」というと，あまり聞き覚えのない方が多いかもしれません．しかし，主張することは非常に単純で直感的なものです．
キルヒホッフの電流則とは「ある点に流入する電流の大きさは，その点から流出する電流の大きさに等しい」ことをいいます．
このことを言いかえると「ある電線を流れている電流はなくならない」となります．
例えば次の回路図をご覧ください．
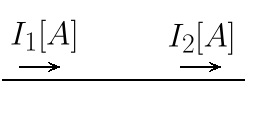この図はある電線の左端から\(I_1[A]\)の大きさの電流が流れ込んできて，右端から\(I_2[A]\)の大きさの電流が流れだしている様子を表しています．この図に対してキルヒホッフの電流則を適用してみましょう．すると，「この電線に流れ込んだ電流\(I_1\)はなくならない」ことになります．したがって，流れ出す電流の大きさ\(I_2[A]\)は流れ込む電流の大きさ\(I_1[A]\)と等しいことになります．つまり，
$$I_1 = I_2$$
となります．
では次のような回路ではどうでしょう？
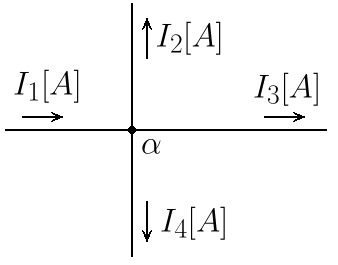この図は，図中央の 点\(\alpha\) に\(I_1[A]\)の大きさの電流が流れ込み，それぞれ上方，右方，下方に\(I_2[A], I_3[A], I_4[A]\)の大きさの電流が流れだしている様子を表しています．この図に対してキルヒホッフの電流則を適用したら\(I_1\)はどのように表せるでしょうか？先ほどの図と同じように考え，「点\(\alpha\)に流れ込んだ電流\(I_1\)はなくならない」のですから，次のようになります．
$$I_1 = I_2 + I_3 + I_4$$
非常に直感的ですが，とても大事な法則です．必ず覚えておきましょう．
オームの法則
オームの法則は，電子回路を知らない人でも，名前だけは知っていることが多い非常に有名な法則です．ご存知の方も多いかとは思いますが，一応確認しておきましょう．
オームの法則は，「抵抗値\(R[\Omega]\)の抵抗に大きさ\(I[A]\)の電流を流したとき，抵抗の両端に発生する電位差\(E\)は\(E=R I[V]\)で表される」ことを，また，「抵抗値\(R[\Omega]\)の抵抗の両端に電位差\(E\)を与えたとき，抵抗を流れる電流\(I[A]\)は\(I=\frac{E}{R}\)で表される」ことを主張します
図で見てみましょう．
この図では，起電力\(V_1[V]\)の電池を抵抗値\(R_1[\Omega]\)の抵抗に接続しており，\(I_1[A]\)の電流が流れています．この\(I_1\)の大きさを求めてみましょう．
…といっても，オームの法則に従って次のように求めます．
$$I_1 = \frac{V_1}{R_1}$$
オームの法則は非常に有名で簡単なものですが，一般的な電子回路の設計では非常に強力な武器になりますので，必ず覚えておきましょう．
さいごに
今回は非常に重要な法則を二つご紹介しました．
これらの法則は話を聞くだけだとそこまで重要性を感じないかもしれませんが，多くの基本的な回路はこの2法則を組み合わせることで解析を行うことが出来ます
次回以降は実際にこれらの法則を使って，回路解析の手法を学んでいくことにしましょう．